在贝叶斯滤波的框架下,卡尔曼滤波的有效性依赖于以下六个关键假设(注:从最小二乘法(Least Squares, LS)的角度推导卡尔曼滤波时,最后两个假设不再必要)。这些假设共同保证了状态估计的高斯分布特性以及递推更新的可解析性:
-[x] 线性系统模型:状态转移和观测模型都必须是线性的。状态的变化和传感器的测量都通过线性方程描述,任何非线性因素都会破坏卡尔曼滤波的精确性。
-[x] 马尔可夫性(无记忆性):当前状态仅依赖于前一时刻的状态,而与更早的历史状态无关;同时,当前的观测值仅依赖于当前的状态。这一特性简化了递推计算,使滤波过程仅需维护当前状态。
-[x] 噪声独立性:过程噪声和观测噪声必须相互独立,并且与初始状态无关。这意味着噪声在不同时间步之间、以及噪声与状态之间没有相关性。
-[x] 已知模型参数:系统的状态转移矩阵、观测矩阵、噪声协方差矩阵等参数必须预先准确已知。如果这些参数不准确或随时间变化,滤波性能会显著下降。
-[x] 高斯噪声分布:过程噪声(系统噪声)和观测噪声(测量噪声)都必须服从零均值的高斯分布。这一假设使得噪声的影响可以用协方差矩阵精确描述,并保证后验概率仍为高斯分布。
-[x] 初始状态的高斯分布:系统的初始状态必须服从高斯分布,即具有已知的均值和协方差矩阵。这样,后续的预测和更新才能保持高斯特性。
这些假设确保了卡尔曼滤波能够以最优(最小均方误差)的方式递推估计状态。
1.时间更新
离散情况:
\[
p(y)=\sum_{x}^{}\left[p(y|x)p(x)\right]
\]
连续情况:
\[
p(y)=\int_{-\infty}^{\infty}p(y|x)p(x)\mathrm{d}x
\]
2.量测更新
离散情况:
\[
p(x_{i}|y)=\frac{p(y|x_{i})p(x_{i})}{\sum_{j}^{}\left [ p(y|x_{j})p(x_{j}) \right ] } =\frac{p(y|x_{i})p(x_{i})}{p(y)}
\]
连续情况:
\[
p(x|y)=\frac{p(y|x)p(x)}{\int_{-\infty}^{\infty}p(y|x)p(x)\mathrm{d}x}=\frac{p(y|x)p(x)}{p(y)}
\]
3.具体的卡尔曼滤波推导
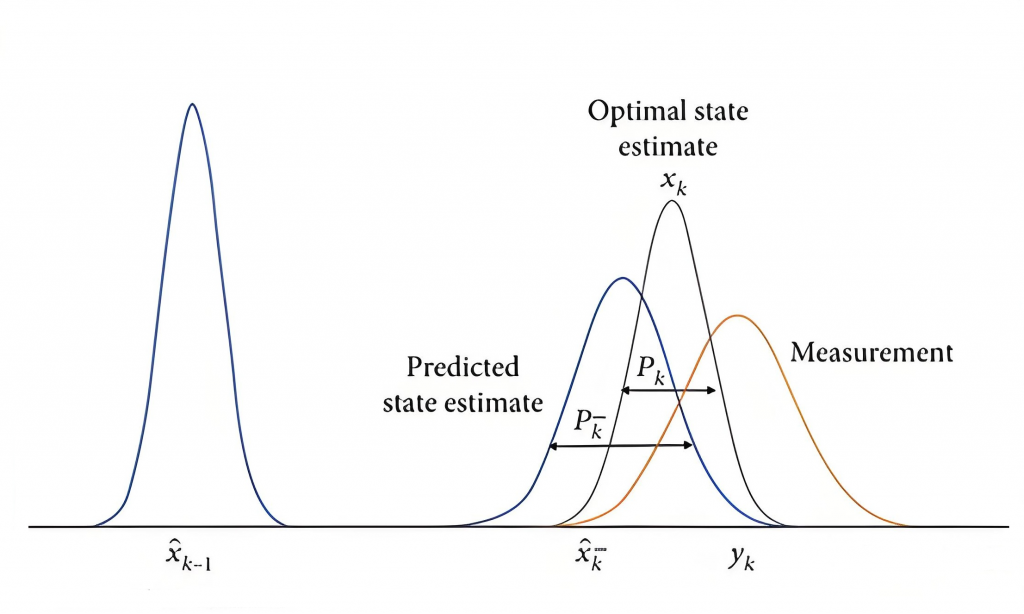
先验=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi Q}} exp\left [ -\frac{(x-Fs)^2}{2Q} \right ] \frac{1}{\sqrt{2\pi P}} exp\left [ -\frac{(s-\bar{x})^2 }{2P} \right ]\mathrm{d}s
\]
上式中的\({\bar{x}}\)表示上一时刻的后验均值,\({P}\)表示上一时刻的后验协方差。
\[后验=\frac{\frac{1}{\sqrt{2\pi R}} exp\left [ -\frac{(y-Hx)^2}{2R} \right ] \frac{1}{\sqrt{2\pi P’}} exp\left [ -\frac{(x-\bar{x}’)^2 }{2P’} \right ]}{\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi R}} exp\left [ -\frac{(y-Hs)^2}{2R} \right ] \frac{1}{\sqrt{2\pi P’}} exp\left [ -\frac{(s-\bar{x}’)^2 }{2P’} \right ]\mathrm{d}s}
\]
上式中的\({\bar{x}’}\)表示当前时刻的先验均值,\({P’}\)表示当前时刻的先验协方差。
Good blog post. I definitely love this site. Thanks!
Fastidious answer back in return of this query with genuine arguments and
describing all concerning that.
Great blog right here! Also your site quite a bit up fast!
What host are you the use of? Can I am getting your affiliate link to
your host? I want my web site loaded up as fast
as yours lol
Quality posts is the secret to attract the viewers to
go to see the website, that’s what this site is providing.
Heya i am for the first time here. I came across
this board and I in finding It truly useful & it helped me out a lot.
I am hoping to offer one thing again and aid others such as you aided
me.
Way cool! Some very valid points! I appreciate you penning this write-up and the rest of the
website is very good.
great points altogether, you simply received a new reader.
What may you recommend about your post that you simply made a few days ago?
Any certain?
Невероятно актуальная разбор,
как раз в это время интересовался ей теме;
)
This information is worth everyone’s attention. Where can I find out
more?
I am really thankful to the holder of this web page who has shared
this wonderful paragraph at here.
Thanks for finally talking about > 2.贝叶斯滤波及贝叶斯角度的卡尔曼滤波 – Kalman Filter < Loved it!
Hello there I am so delighted I found your site, I really found
you by error, while I was researching on Askjeeve for something else,
Anyways I am here now and would just like to say kudos for a incredible
post and a all round thrilling blog (I also love the theme/design), I don’t have time to look
over it all at the minute but I have saved it and also included your RSS feeds, so when I have time I
will be back to read much more, Please do keep up the excellent jo.
WOW just what I was looking for. Came here by searching for free
apps post a comment
It’s really a nice and helpful piece of information. I am
glad that you simply shared this useful information with
us. Please stay us up to date like this. Thanks for sharing.
My brother recommended I would possibly like this blog.
He was once totally right. This submit actually made my day.
You cann’t consider just how much time I had spent for
this info! Thanks!
First of all I want to say excellent blog!
I had a quick question that I’d like to ask if you
don’t mind. I was interested to find out how
you center yourself and clear your thoughts prior to writing.
I have had a difficult time clearing my mind in getting my thoughts out.
I do enjoy writing however it just seems like the first 10 to 15 minutes tend to be wasted simply just
trying to figure out how to begin. Any suggestions or tips?
Thanks!
It is appropriate time to make some plans for the future and it’s time to be happy.
I have read this post and if I could I wish to suggest you few interesting things or advice.
Perhaps you can write next articles referring to this article.
I wish to read more things about it!