无迹卡尔曼滤波 (Unscented Kalman Filter, UKF) 是一种高效的非线性滤波算法,由Julier和Uhlmann于1997年提出。它通过无迹变换 (Unscented Transform) 来处理非线性系统的状态估计问题,克服了扩展卡尔曼滤波 (EKF) 在强非线性系统中精度不足的问题。
基本原理
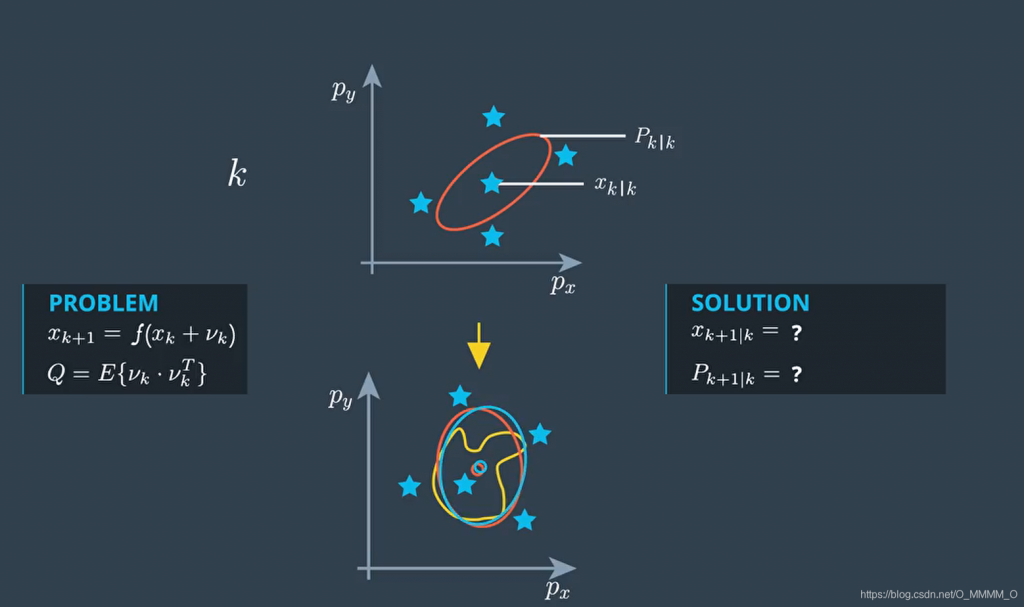
无迹变化
无迹变换的核心思想是:近似概率分布比近似非线性函数更容易,通过选择一组代表性的点(如sigma点),这些点捕获了输入分布的均值和协方差,然后将这些点通过非线性函数传播,最后从传播后的点计算输出分布的统计量(均值、协方差等)。
UKF通过对称的点阵生成方式,采用球面-径向规则选择sigma点。对于n维随机变量x,其均值为\(\bar{x}\),协方差为\(P_{xx}\),UKF生成\(2n\)个sigma点,\(\sqrt{P_{xx}}\)是一个下三角矩阵,满足\(\sqrt{P_{xx}} (\sqrt{P_{xx}})^T=P_{xx}\)。
\[\begin{aligned}
\chi_i &= \bar{x} + \sqrt{P_{xx}} \xi_i, \quad i=1,\dots,2n \\
\xi_i &= \sqrt{n} \mathbf{e}_i ,\quad i=1,\dots,n\\
\xi_{i+n} &= -\sqrt{n} \mathbf{e}_i ,\quad i=1,\dots,n
\end{aligned}
\]
这里 \(\mathbf{e}_i\) 是n维单位向量在第i个方向上的向量。当维度为4时,\(\mathbf{e}_1=\begin{bmatrix}1 & 0 & 0 & 0\end{bmatrix}^T\),\(\mathbf{e}_2=\begin{bmatrix}0 & 1 & 0 & 0\end{bmatrix}^T\)。
所有sigma点具有相同的权重:
\[W_i = \frac{1}{2n}, \quad i=1,\dots,2n
\]
这种对称的权重分配保证了数值稳定性和计算效率。
UKF算法步骤
1. 初始化
\[\begin{aligned}
\hat{x}_0 &= E[x_0] \\
P_0 &= E[(x_0-\hat{x}_0)(x_0-\hat{x}_0)^T]
\end{aligned}
\]
2. 时间更新(预测步骤)
基于状态向量生成sigma点:
\chi_{k-1} = [\hat{x}_{k-1} + \sqrt{P_{k-1}} \xi_1, \dots, \hat{x}_{k-1} + \sqrt{P_{k-1}} \xi_{2n}]
\]
状态预测:
\[
\begin{aligned}
\chi_{k|k-1}^* &= f(\chi_{k-1}, u_{k-1}) \\
\hat{x}_k^- &= \frac{1}{2n} \sum_{i=1}^{2n} \chi_{i,k|k-1}^* \\
P_k^- &= \frac{1}{2n} \sum_{i=1}^{2n} [\chi_{i,k|k-1}^* – \hat{x}_k^-][\chi_{i,k|k-1}^* – \hat{x}_k^-]^T + Q_k
\end{aligned}
\]
3. 测量更新
重新生成sigma点进行观测预测,基于预测状态重新生成sigma点:
\chi_{k|k-1} = [\hat{x}_k^- + \sqrt{P_k^-} \xi_1, \dots, \hat{x}_k^- + \sqrt{P_k^-} \xi_{2n}]
\]
观测预测:
\[\begin{aligned}
\mathcal{Z}_{k|k-1} &= h(\chi_{k|k-1}) \\
\hat{z}_k^- &= \frac{1}{2n} \sum_{i=1}^{2n} \mathcal{Z}_{i,k|k-1} \\
P_{z_k z_k} &= \frac{1}{2n} \sum_{i=1}^{2n} [\mathcal{Z}_{i,k|k-1} – \hat{z}_k^-][\mathcal{Z}_{i,k|k-1} – \hat{z}_k^-]^T + R_k \\
P_{x_k z_k} &= \frac{1}{2n} \sum_{i=1}^{2n} [\chi_{i,k|k-1} – \hat{x}_k^-][\mathcal{Z}_{i,k|k-1} – \hat{z}_k^-]^T
\end{aligned}
\]
卡尔曼增益和状态更新:
\[\begin{aligned}
K_k &= P_{x_k z_k} P_{z_k z_k}^{-1} \\
\hat{x}_k &= \hat{x}_k^- + K_k(z_k – \hat{z}_k^-) \\
P_k &= P_k^- – K_k P_{z_k z_k} K_k^T
\end{aligned}
\]
总结
UKF通过对称的sigma点采样和重新生成策略,在保持计算效率的同时显著提高了非线性系统的估计精度。其数值稳定性和实现简便性使其在机器人导航、目标跟踪、金融建模等领域的实际应用中表现出色,是现代非线性估计理论中的重要进展。